Two-dimensional field-resolved spectroscopy of Landau electrons reveals population inversion and multiwave mixing that are explained by Coulomb interactions between electrons and the ionic background.
http://spie.org/newsroom/6634-extending-nonlinear-coherent-quantum-control-with-intense-terahertz-pulses
http://spie.org/newsroom/6634-extending-nonlinear-coherent-quantum-control-with-intense-terahertz-pulses
19 October 2016, SPIE Newsroom. DOI: 10.1117/2.1201608.006634
Dynamics in solid-state systems are governed by many-body interactions that are inherently tied to the high density of electrons and ions. For most elementary excitations, however, Coulomb (i.e., elastic) scattering leads to dephasing within a few to a few-hundreds of femtoseconds. Coherent quantum control (the precise manipulation of the phases of quantum states) is therefore usually considered to be a daunting challenge in many-body systems.
In 1961, however, Walter Kohn found that the cyclotron resonance (CR) of Landau electrons (i.e., the harmonic motion of electrons in a magnetic field) is immune to electron–electron Coulomb interactions. Kohn's theorem thus shows that the CR is one of the most robust manifestations of the quantum harmonic oscillator, and excludes the possibility of any nonlinear light–matter interactions.1 Although the CR has given rise to a number of sophisticated quantum phenomena, such as ultrastrong light–matter coupling,2 superradiance,3 coherent control,4 and superfluorescence,5 the complete absence of nonlinearities suggests that many intriguing possibilities (e.g., quantum logic operations) are excluded.
In this work,6 we show how strong terahertz (THz) pulses can be used to create non-perturbative THz excitations of a magnetically biased, 2D electron gas (2DEG). The pulses induce strong, coherent nonlinearities and facilitate coherent quantum control of multiple Landau levels, leading to population inversion. In our approach, the 2DEG is contained within two 30nm-wide gallium arsenide quantum wells (each n-doped at 1.6 × 1011cm−2) and is biased with a perpendicular magnetic field of 3.5T. These conditions provide a filling factor of 0.95 and a CR frequency (νc) of 1.45THz.
In our experiments, strong linearly polarized THz transients—which are incident perpendicular to the sample—cause the excitation of a coherent polarization. We monitor this polarization by examining the orthogonal polarization component of the reradiated field, as illustrated in Figure 1(a). For weak THz transients with an amplitude of 0.7kVcm−1 (black curve), we observe long-lived coherent oscillations. When we increase the field up to 8.7kVcm−1 (red curve), however, we find that the coherence is strongly diminished. By fitting an exponentially decaying sinusoidal function to the data, we extract the 1/e decay constant (τc) and find—see Figure 1(b)—that there is an abrupt drop in the coherence at about 3kVcm−1. We use a microscopic many-body theory to calculate the dynamics of the electrons. In this way, we retrieve the Landau-level population as a function of THz amplitude—blue and red bars in the inset of Figure 1(b)—which reveals that interactions with longitudinal optical phonons lead to the sharp drop of coherence. Furthermore, our theory shows that the population climbs up to the 6th Landau level and that population inversion is achieved.
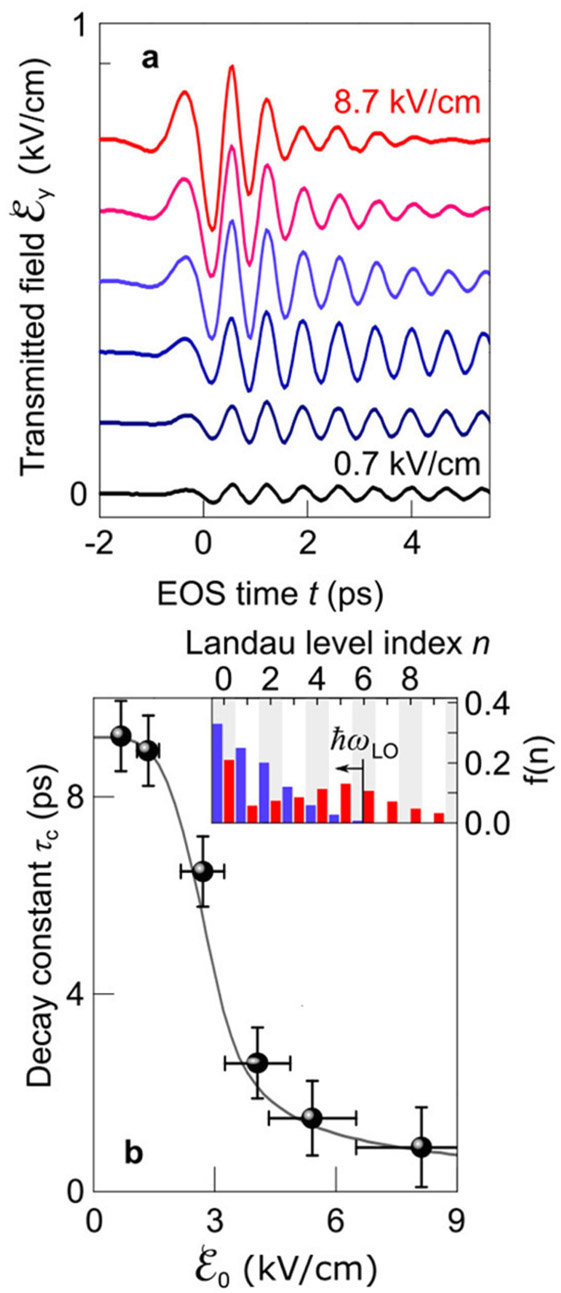
Figure 1. (a) The transmitted terahertz (THz) field is used to monitor the coherent inter-Landau level polarization. Results are shown for different amplitudes of the driving field (between 0.7 and 8.7kVcm- 1), as a function of the electro-optic sampling (EOS) delay time (t). (b) The decay constant (τc) that is extracted from the data in (a), as a function of the initial field (
). The Landau-level population, for fields of 4.3 and 8.7kVcm-1 (blue and red bars, respectively), is shown in the inset. f: Population density. ℏωLO: Longitudinal optical phonon energy.
). The Landau-level population, for fields of 4.3 and 8.7kVcm-1 (blue and red bars, respectively), is shown in the inset. f: Population density. ℏωLO: Longitudinal optical phonon energy.
To systematically test whether coherent nonlinear control of massively many-body Landau states is possible, we perform 2D, phase-resolved THz spectroscopy. To this end, we use a strong, single-cycle THz pulse (A) to create a highly excited coherent state, and a weak pulse (B) to probe the quantum state of the CR. We then measure the coherent polarization dynamics as a function of the electro-optic sampling time (t) of B, as well as the relative delay (τ) between the pulses. If Kohn's theorem applies, the correlated nonlinear polarization response (
)—i.e., representing the interactions between A and B—should be zero, as verified for small amplitudes of the electric field (
).6 However, strong coherent modulations in occur at multiples of νc−1 along both time axes (i.e., τ and t) even for moderate values of —see Figure 2(a) and (b)—of 1.4 and 4.3kVcm−1. These wavefronts in the time domain are linked to distinct features in the frequency domain that represent the pump-probe, as well as four- and six-wave mixing processes. Furthermore, the relative amplitudes of the off-diagonal pump-probe and four-wave mixing signals are evidence of the non-perturbative scaling exhibited by the surprisingly strong nonlinearities.6
)—i.e., representing the interactions between A and B—should be zero, as verified for small amplitudes of the electric field ().6 However, strong coherent modulations in occur at multiples of νc−1 along both time axes (i.e., τ and t) even for moderate values of —see Figure 2(a) and (b)—of 1.4 and 4.3kVcm−1. These wavefronts in the time domain are linked to distinct features in the frequency domain that represent the pump-probe, as well as four- and six-wave mixing processes. Furthermore, the relative amplitudes of the off-diagonal pump-probe and four-wave mixing signals are evidence of the non-perturbative scaling exhibited by the surprisingly strong nonlinearities.6
Figure 2. (a) and (b) The nonlinear THz polarization response, 
, for two representative field amplitudes () of pulse A. Example wavefronts that represent a pump-probe (black line) and a four-wave mixing process (red line) are indicated in (a). (c) and (d) Fourier transformation of the data from (a) and (b), as a function of the frequencies νt and ντ. The pump-probe (PP), four-wave mixing (4WM), and six-wave mixing (6WM) signatures are circled.
, for two representative field amplitudes () of pulse A. Example wavefronts that represent a pump-probe (black line) and a four-wave mixing process (red line) are indicated in (a). (c) and (d) Fourier transformation of the data from (a) and (b), as a function of the frequencies νt and ντ. The pump-probe (PP), four-wave mixing (4WM), and six-wave mixing (6WM) signatures are circled.
Our microscopic theory allows us to assess the relative contributions of the nonlinearities by making a ‘switch-off’ analysis.6 The results of this analysis reveal that band-structure effects are initially dominant (at of 1.4kVcm−1), but are overruled by much stronger, many-body interactions between electrons and dopant ions that occur as increases. These Coulomb effects thus dynamically gain strength with increasing and induce a range of fully coherent nonlinearities. It is such nonlinearities that are responsible for the non-perturbative four- and six-wave mixing signals in this setting (i.e., beyond the realm of Kohn's theorem).
of 1.4kVcm−1), but are overruled by much stronger, many-body interactions between electrons and dopant ions that occur as increases. These Coulomb effects thus dynamically gain strength with increasing and induce a range of fully coherent nonlinearities. It is such nonlinearities that are responsible for the non-perturbative four- and six-wave mixing signals in this setting (i.e., beyond the realm of Kohn's theorem).
In summary, we have demonstrated that strong terahertz pulses can be used to create strong, coherent nonlinearities in Landau systems that are suitable for THz quantum control. Our results show that the cyclotron resonance is a promising candidate for quantum control at THz clock rates as it provides both the long-lived coherence and nonlinearities that are required for switching operations. In more general terms, Coulomb correlations are used to examine the internal degrees of freedom of many-body quantum systems. Our work suggests that the role of massive many-body interactions (usually considered as detrimental to quantum control) will have to be reassessed. Currently, we are investigating coherent quantum control of Landau electrons in non-polar semiconductors, in which an even larger number of Landau levels may contribute to the nonlinearity before phonon interactions become relevant.
Christoph Lange, Thomas Maag, Andreas Bayer, Sebastian Baierl, Matthias Hohenleutner, Dieter Schuh, Dominique Bougeard, Rupert Huber
Department of PhysicsUniversity of Regensburg
Regensburg, Germany
Martin Mootz, Stephan Koch, Mackillo Kira
Department of PhysicsUniversity of Marburg
Marburg, Germany
John Sipe
Department of PhysicsUniversity of Toronto
Toronto, Canada
References:
1. W. Kohn, Cyclotron resonance and de Haas-van Alphen oscillations of an interacting electron gas, Phys. Rev. 123, p. 1242-1244, 1961.
2. G. Scalari, C. Maissen, D. Turčinková, D. Hagenmüller, S. De Liberato, C. Ciuti, C. Reichl, et al., Ultrastrong coupling of the cyclotron transition of a 2D electron gas to a THz metamaterial, Science 335, p. 1323-1326, 2012.
3. Q. Zhang, T. Arikawa, E. Kato, J. L. Reno, W. Pan, J. D. Watson, M. J. Manfra, et al., Superradiant decay of cyclotron resonance of two-dimensional electron gases, Phys. Rev. Lett. 113, p. 047601, 2014. doi:10.1103/PhysRevLett.113.047601
4. T. Arikawa, X. Wang, D. J. Hilton, J. L. Reno, W. Pan, J. Kono, Quantum control of a Landau-quantized two-dimensional electron gas in a GaAs quantum well using coherent terahertz pulses, Phys. Rev. B 84, p. 241307(R), 2011. doi:10.1103/PhysRevB.84.241307
5. G. T. Noe II, J.-H. Kim, J. Lee, Y. Wang, A. K. Wójcik, S. A. McGill, D. H. Reitze, A. A. Belyanin, J. Kono, Giant superfluorescent bursts from a semiconductor magneto-plasma,Nat. Phys. 8, p. 219-224, 2012.
6. T. Maag, A. Bayer, S. Baierl, M. Hohenleutner, T. Korn, C. Schüller, D. Schuh, et al., Coherent cyclotron motion beyond Kohn's theorem, Nat. Phys. 12, p. 119-123, 2016.
No comments:
Post a Comment
Please share your thoughts. Leave a comment.